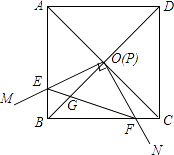
如图，边长为1的正方形ABCD的对角线AC、BD相交于点O．有直角∠MPN，使直角顶点P与点O重合，直角边PM、PN分别与OA、OB重合，然后逆时针旋转∠MPN，旋转角为θ（0°＜θ＜90°），PM、PN分别交AB、BC于E、F两点，连接EF交OB于点G，则下列结论中正确的是．①EF= OE；②S四边形OEBF：S正方形ABCD=1：4；③BE+BF= OA；④在旋转过程中，当△BEF与△COF的面积之和最大时，AE= ；⑤OG•BD=AE2+CF2 ．

①定义：各角对应相等，各边对应成比例的两个三角形．

②平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似．

③有两个角对应相等．

④两边对应成比例，且夹角相等．

⑤三边对应成比例．

⑥在直角三角形中，斜边和一条直角边对应成比例．

①对应角，对应边.

②周长之比等于；面积之比等于.

③对应高线长之比、对应角平分线长之比、对应中线长之比都等于.

基础知识填空容易

填空题容易

判定1	平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似.
判定2	三边对应的两个三角形相似.
判定3	两边对应成比例且夹角的两个三角形相似.
判定4	两角分别的两个三角形相似.

基础知识填空容易

填空题普通

填空题普通

填空题普通

单选题困难

解答题容易

单选题容易

$\text{[math]}$ 求证： $\text{[math]}$ ；

$\text{[math]}$ 连结 $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ ，直接写出 $\text{[math]}$ ▲ ；

综合题困难

2. 已知，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 上一点，满足： $\text{[math]}$ ；将 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ．