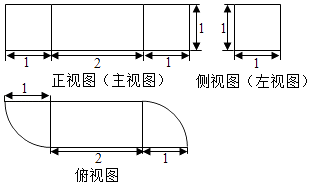
1.
设甲、乙两个圆柱的底面积分别为S1 , S2 , 体积分别为V1 , V2 , 若它们的侧面积相等,且  =
=  ,则
,则  的值是.
的值是.
【考点】
旋转体(圆柱/圆锥/圆台/球)的结构特征;
棱柱、棱锥、棱台的体积;