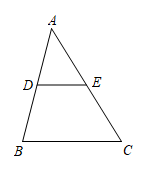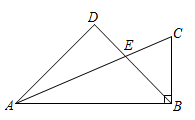
如图，△ABC中，∠A＝78°，AB＝4，AC＝6．将△ABC沿图示中的虚线剪开，剪下的阴影三角形与原三角形不相似的是（）

1. 如图，已知△ABC与△BDE都是等边三角形，点D在边AC上（不与点A、C重合），DE与AB相交于点F，那么与△BFD相似的三角形是（　　　）

单选题容易

2. 如图，D是 $\text{[math]}$ 的边BC上的一点，那么下列四个条件中，不能够判定△ABC与△DBA相似的是（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易

3. 能判定 $\text{[math]}$ 与 $\text{[math]}$ 相似的条件是（）

A. $\text{[math]}$ B. $\text{[math]}$ ，且 $\text{[math]}$ C. $\text{[math]}$ 且 $\text{[math]}$ D. $\text{[math]}$ ，且 $\text{[math]}$

单选题容易

1. 如图，在 $\text{[math]}$ 中，点 $\text{[math]}$ 在边 $\text{[math]}$ 上，则下列四个条件： ① $\text{[math]}$ ； ② $\text{[math]}$ $\text{[math]}$ ； ③ $\text{[math]}$ ； ④ $\text{[math]}$ $\text{[math]}$ ，其中，不能判定 $\text{[math]}$ 与 $\text{[math]}$ 相似的是（）

A. ① B. ② C. ③ D. ④

单选题普通

2. 如图，点 $\text{[math]}$ 在 $\text{[math]}$ 的边 $\text{[math]}$ 上，添加一个条件，使得 $\text{[math]}$ .以下是天翼和徍琛的做法.下列说法不正确的是（）

天翼的做法：添加条件 $\text{[math]}$ .

证明： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .（两组角对应相等的两个三角形相似）

徍琛的做法：添加条件 $\text{[math]}$ .

证明： $\text{[math]}$ ， $\text{[math]}$ ，

$\text{[math]}$ .（两组对应边成比例及一组对应角相等的两个三角形相似）

A. 天翼的做法证明过程没有问题 B. 徍琛的做法证明过程没有问题 C. 天翼的做法添加的条件没有问题 D. 徍琛的做法添加的条件有问题

单选题普通

3. 如图，在小正方形的边长为1的网格中，三角形的顶点都在格点上，与 $\text{[math]}$ 相似的是（）

单选题普通

1. 如图，在 $\text{[math]}$ 中，点D ， E分别在边 $\text{[math]}$ 上．添加一个条件使 $\text{[math]}$ ，则这个条件可以是．（写出一种情况即可）

填空题容易

2.

判定1	平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似.
判定2	三边对应的两个三角形相似.
判定3	两边对应成比例且夹角的两个三角形相似.
判定4	两角分别的两个三角形相似.

基础知识填空容易

3. 如图，要使△AFE∽△ABC ，可以添加条件：．

填空题容易

1. 综合与实践

“善思”小组开展“探究四点共圆的条件”活动，得出结论：对角互补的四边形四个顶点共圆．该小组继续利用上述结论进行探究．

提出问题：

如图1，在线段AC同侧有两点B ， D ，连接AD ， AB ， BC ， CD ，如果∠B＝∠D ，那么A ， B ， C ， D四点在同一个圆上．

探究展示：

如图2，作经过点A ， C ， D的⊙O ，在劣弧AC上取一点E（不与A ， C重合），连接AE ， CE ，则∠AEC+∠D＝180°（依据1）

∵∠B＝∠D

∴∠AEC+∠B＝180°

∴点A ， B ， C ， E四点在同一个圆上（对角互补的四边形四个顶点共圆）

∴点B ， D在点A ， C ， E所确定的⊙O上（依据2）

∴点A ， B ， C ， D四点在同一个圆上

(1) 反思归纳：

上述探究过程中的“依据1”、“依据2”分别是指什么？

依据1：；依据2：．

(2) 如图3，在四边形ABCD中，∠1＝∠2，∠3＝45°，则∠4的度数为．

(3) 拓展探究：

如图4，已知△ABC是等腰三角形，AB＝AC ，点D在BC上（不与BC的中点重合），连接AD ．作点C关于AD的对称点E ，连接EB并延长交AD的延长线于F ，连接AE ， DE ．

①求证：A ， D ， B ， E四点共圆；

②若AB＝2 $\text{[math]}$ ， AD•AF的值是否会发生变化，若不变化，求出其值；若变化，请说明理由．

实践探究题困难

2. 如图

(1) 【问题背景】已知D、E分别是 $\text{[math]}$ 的AB边和AC边上的点，且 $\text{[math]}$ ，则 $\text{[math]}$ ，把 $\text{[math]}$ 绕着 $\text{[math]}$ 逆时针方向旋转，连接BD和CE.

①如图2，找出图中的另外一组相似三角形

②若AB=8，AC=6，BD=4，则CE=

(2) 【迁移应用】如图3，在Rt $\text{[math]}$ 和Rt $\text{[math]}$ 中， $\text{[math]}$ $\text{[math]}$ ，点 $\text{[math]}$ 是线段BC上一动点，连接EC

①请求出 $\text{[math]}$ 的值及 $\text{[math]}$ 的度数，并说明理由.

②如图4，点 $\text{[math]}$ 是DE的中点，在点 $\text{[math]}$ 从 $\text{[math]}$ 点运动到 $\text{[math]}$ 点的过程中，请直接写出点 $\text{[math]}$ 经过的路径长.

(3) 【创新应用】如图5： $\text{[math]}$ 是直角三角形， $\text{[math]}$ $\text{[math]}$ ，将 $\text{[math]}$ 绕若点 $\text{[math]}$ 旋转，连接BE，F是BE上一点， $\text{[math]}$ ，连接CF，求CF的取值范围.

实践探究题困难

3. 【问题初探】数学课上，老师提出如下问题：

如图1，在矩形ABCD中，点E，F分别是AD，CD的中点，AF与BE相交于点G，求AG的值经过思考，小明同学和小慧同学分别给出如下解题思路：

小明：可以过中点作平行线，过点E作EH//AB交AF于点H，如图2所示，或者过点F作FK∥AD交A8于点K，交BE于点Q，如图3所示.

小慧：还可以延长中点所在的线段，如图4，延长BE交CD的延长线于点P.

(1) 请根据上述两位同学的思路，选择其中一种思路，求出 $\text{[math]}$ 的值.

(2) 【类比分析】

老师发现两位同学都利用了转化思想，为了帮助同学们更好地利用转化思想解决问题，老师改变题中的条件，如图5，将图1中的矩形ABCD改成菱形ABCD，其余条件不变，那么 $\text{[math]}$ 的值是否改变?请说明理由.

(3) 【学以致用】

如图6，已知正方形ABCD中心为点 $\text{[math]}$ ，边长为4，另一边长为 $\text{[math]}$ 的正方形EFGH的中心与点 $\text{[math]}$ 重合，连接CE，设CE的中点为 $\text{[math]}$ ，将正方形EFGH绕点 $\text{[math]}$ 旋转，当A，E，F三点恰好在同一直线上时，请直接写出OM的长.