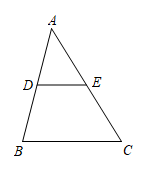如图，点在的边上，添加一个条件，使得.以下是天翼和徍琛的做法.下列说法不正确的是（）天翼的做法：添加条件.证明：，， .（两组角对应相等的两个三角形相似）徍琛的做法：添加条件.证明：，， .（两组对应边成比例及一组对应角相等的两个三角形相似）

0 返回首页

1. 如图，点 $\text{[math]}$ 在 $\text{[math]}$ 的边 $\text{[math]}$ 上，添加一个条件，使得 $\text{[math]}$ .以下是天翼和徍琛的做法.下列说法不正确的是（）

天翼的做法：添加条件 $\text{[math]}$ .

证明： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .（两组角对应相等的两个三角形相似）

徍琛的做法：添加条件 $\text{[math]}$ .

证明： $\text{[math]}$ ， $\text{[math]}$ ，

$\text{[math]}$ .（两组对应边成比例及一组对应角相等的两个三角形相似）

A. 天翼的做法证明过程没有问题 B. 徍琛的做法证明过程没有问题 C. 天翼的做法添加的条件没有问题 D. 徍琛的做法添加的条件有问题

【考点】

相似三角形的判定;

【答案】

您现在未登录，无法查看试题答案与解析。登录

单选题普通

基础巩固

能力提升

变式训练

拓展培优

真题演练

换一批

1. 如图，已知△ABC与△BDE都是等边三角形，点D在边AC上（不与点A、C重合），DE与AB相交于点F，那么与△BFD相似的三角形是（　　　）

A. △BFE； B. △BDC； C. △BDA； D. △AFD．

单选题容易

2. 如图，D是 $\text{[math]}$ 的边BC上的一点，那么下列四个条件中，不能够判定△ABC与△DBA相似的是（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易

3. 能判定 $\text{[math]}$ 与 $\text{[math]}$ 相似的条件是（）

A. $\text{[math]}$ B. $\text{[math]}$ ，且 $\text{[math]}$ C. $\text{[math]}$ 且 $\text{[math]}$ D. $\text{[math]}$ ，且 $\text{[math]}$

单选题容易

1. 如图，在 $\text{[math]}$ 中，点 $\text{[math]}$ 在边 $\text{[math]}$ 上，则下列四个条件： ① $\text{[math]}$ ； ② $\text{[math]}$ $\text{[math]}$ ； ③ $\text{[math]}$ ； ④ $\text{[math]}$ $\text{[math]}$ ，其中，不能判定 $\text{[math]}$ 与 $\text{[math]}$ 相似的是（）

A. ① B. ② C. ③ D. ④

单选题普通

2. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，将 $\text{[math]}$ 沿图中的虚线前开，前下的阴影三角形与原三角形不相似的是（）

单选题普通

3. 如图，在小正方形的边长为1的网格中，三角形的顶点都在格点上，与 $\text{[math]}$ 相似的是（）

单选题普通

1. 如图，在 $\text{[math]}$ 中，点D ， E分别在边 $\text{[math]}$ 上．添加一个条件使 $\text{[math]}$ ，则这个条件可以是．（写出一种情况即可）

填空题容易

判定1	平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似.
判定2	三边对应的两个三角形相似.
判定3	两边对应成比例且夹角的两个三角形相似.
判定4	两角分别的两个三角形相似.

基础知识填空容易

3. 如图，要使△AFE∽△ABC ，可以添加条件：．

填空题容易

1. 如图，点 E、F、G、H分别是 $\text{[math]}$ 各边的中点，连接AF、CE 相交于点M，连接AG、CH相交于点 N，且AM=AN.

(1) 求证：四边形AMCN 是菱形；

(2) 若△AEM的面积为2，求四边形AMCN 的面积.

解答题普通

2. 综合与实践课上，徐老师和同学们开展了一场以“最小值”为主题的探究活动．

【提出问题】徐老师提出了一个问题：如图1，在矩形ABCD中， $\text{[math]}$ ， $\text{[math]}$ ， P为AD边上的一动点，以PC为边向右作等边 $\text{[math]}$ ，连接BE ，如何求BE的最小值?

【探究发现】小亮发现：如图4所示，以BC为边向下构造一个等边 $\text{[math]}$ ，便可得到 $\text{[math]}$ ，进而将BE的最小值转化为PM的最小值的问题．

(1) 按照小明的想法，求证： $\text{[math]}$ ；并求出BE的最小值．

(2) 【拓展应用】

小刚受此启发，举一反三，提出新问题：如图2，若将图1当中构造的等边三角形，改为以PC为边向右构造正方形PCFG ，在运动过程中，求出BG的最小值．

(3) 小红同学深入研究了小刚的问题，并又提出了新的问题：如图3，若将图2当中构造的正方形改为以PC为边向右构造菱形PCHI ，使 $\text{[math]}$ ，也可求得BI的最小值．请你直接写出BI最小值为．

实践探究题困难

3. 综合与实践

在一次综合实践活动课上，王老师给每位同学各发了一张正方形纸片，请同学们思考如何仅通过折纸的方法来确定正方形一边上的一个三等分点．

【操作探究】

“乘风”小组的同学经过一番思考和讨论交流后，进行了如下操作：

第 $\text{[math]}$ 步：如图 $\text{[math]}$ 所示，先将正方形纸片 $\text{[math]}$ 对折，使点 $\text{[math]}$ 与点 $\text{[math]}$ 重合，然后展开铺平，折痕为 $\text{[math]}$ ；

第 $\text{[math]}$ 步：将 $\text{[math]}$ 边沿 $\text{[math]}$ 翻折到 $\text{[math]}$ 的位置；

第 $\text{[math]}$ 步：延长 $\text{[math]}$ 于点 $\text{[math]}$ ，则点 $\text{[math]}$ 边的三等分点．

证明过程如下：连接 $\text{[math]}$ ，

$\text{[math]}$ 正方形 $\text{[math]}$ 折叠，

$\text{[math]}$ ▲ ，

又 $\text{[math]}$ ，

$\text{[math]}$ ，

$\text{[math]}$ ．

由题意可知 $\text{[math]}$ 的中点，设 $\text{[math]}$ 个单位 $\text{[math]}$ ，则 $\text{[math]}$ ，

在 $\text{[math]}$ 中，可列方程： $\text{[math]}$ ▲ ， $\text{[math]}$ 方程不要求化简 $\text{[math]}$

解得： $\text{[math]}$ ▲ ，即 $\text{[math]}$ 边的三等分点．

“破浪”小组是这样操作的：

第 $\text{[math]}$ 步：如图 $\text{[math]}$ 所示，先将正方形纸片对折，使点 $\text{[math]}$ 与点 $\text{[math]}$ 重合，然后展开铺平，折痕为 $\text{[math]}$ ；

第 $\text{[math]}$ 步：再将正方形纸片对折，使点 $\text{[math]}$ 与点 $\text{[math]}$ 重合，再展开铺平，折痕为 $\text{[math]}$ ，沿 $\text{[math]}$ 翻折得折痕 $\text{[math]}$ 于点 $\text{[math]}$ ；

第 $\text{[math]}$ 步：过点 $\text{[math]}$ 折叠正方形纸片 $\text{[math]}$ ，使折痕 $\text{[math]}$ ．

【过程思考】

(1) “乘风”小组的证明过程中，三个空的所填的内容分别是

$\text{[math]}$ ：， $\text{[math]}$ ：， $\text{[math]}$ ：；

(2) 结合“破浪”小组操作过程，判断点 $\text{[math]}$ 是否为 $\text{[math]}$ 边的三等分点，并证明你的结论；

(3) 【拓展提升】

如图 $\text{[math]}$ ，在菱形 $\text{[math]}$ 中， $\text{[math]}$ 上的一个三等分点，记点 $\text{[math]}$ 关于 $\text{[math]}$ 的对称点为 $\text{[math]}$ ，射线 $\text{[math]}$ 与菱形 $\text{[math]}$ 的边交于点 $\text{[math]}$ ，请直接写出 $\text{[math]}$ 的长．