1.
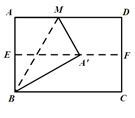
如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF.把纸片展平,再一次折叠纸片,使点A落在EF上的点A′处,并使折痕经过点B,得到折痕BM.若矩形纸片的宽AB=4,则折痕BM的长为( )
A.
 B.
B.
 C.
8
D.
C.
8
D.

【考点】
含30°角的直角三角形;
翻折变换(折叠问题);
锐角三角函数的定义;
基础巩固
能力提升
变式训练
拓展培优