1.
在△ABC中，AB = AC，∠ABC = 30°，△BDE是等边三角形，连接CD、AE.
(1)
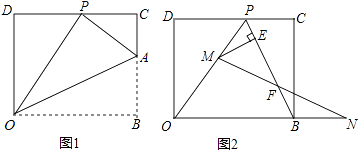
如图1，当A、B、D三点在同一直线上时，AE、BC交于点P，且AE⊥AC.若PC = 4，求PE的长；
(2)
如图2，当B、E、C三点在同一直线上时，F是CD中点，连接AF、EF，求证：AE = 2AF ；
(3)
如图3，在（2）的条件下，AB=8，E在直线BC上运动，将△AEF沿EF翻折得到△MEF，连接DM，G是AB上一点，且BG=
AB，O是直线BC上的另一个动点，连接OG，将△BOG沿OG翻折得到△HOG，连接HM，当HM最小时，直接写出此时点D到直线EM的距离.
【考点】
等边三角形的判定与性质;
含30°角的直角三角形;
翻折变换（折叠问题）;
相似三角形的判定与性质;
锐角三角函数的定义;
三角形全等的判定-SAS;
能力提升
