1.
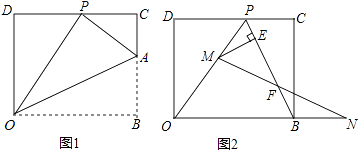
在平面直角坐标系中,O为原点,点B在x轴的正半轴上,D(0,8),将矩形OBCD折叠,使得顶点B落在CD边上的P点处.
(1)
如图①,已知折痕与边BC交于点A,若OD=2CP,求点A的坐标.
(2)
若图①中的点 P 恰好是CD边的中点,求∠AOB的度数.
(3)
如图②,在(I)的条件下,擦去折痕AO,线段AP,连接BP,动点M在线段OP上(点M与P,O不重合),动点N在线段OB的延长线上,且BN=PM,连接MN交PB于点F,作ME⊥BP于点E,试问当点M,N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;若不变,求出线段EF的长度(直接写出结果即可
【考点】
翻折变换(折叠问题);