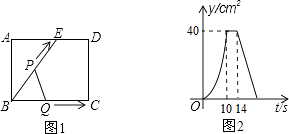1.
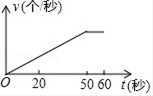
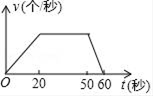
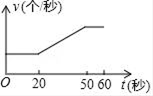
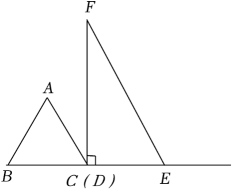
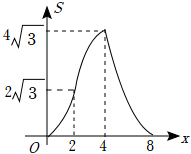
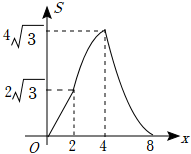
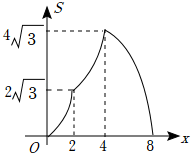
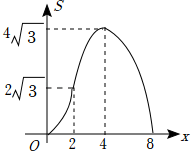
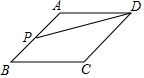
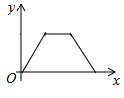
如图,点P是菱形ABCD边上的动点,它从点A出发沿A→B→C→D路径匀速运动到点D , 设  的面积为y , P点的运动时间为x , 则y关于x的函数图象大致为( )
的面积为y , P点的运动时间为x , 则y关于x的函数图象大致为( )
A.
 B.
B.
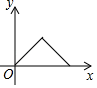 C.
C.
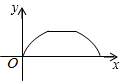 D.
D.
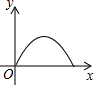
 B.
B.
 C.
C.
 D.
D.

【考点】
分段函数;
动点问题的函数图象;