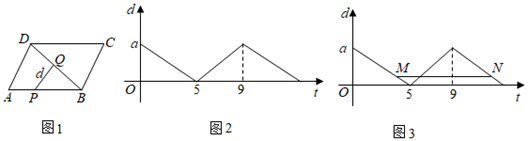
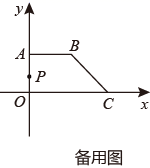
如图，在平面直角坐标系中，点A坐标为（0，3），点C坐标为（6，0），AB x轴，且OA=AB，动点P从点O出发以2个单位/秒的速度沿O→A→B→C的路线匀速运动，运动到点C时终止．过点P作PQ⊥x轴，垂足为Q，设点P的运动时间为x（s），线段PQ的长为y．

1. 如图，在平面直角坐标系中，点A坐标为（0，3），点C坐标为（6，0），AB $\text{[math]}$ x轴，且OA=AB，动点P从点O出发以2个单位/秒的速度沿O→A→B→C的路线匀速运动，运动到点C时终止．过点P作PQ⊥x轴，垂足为Q，设点P的运动时间为x（s），线段PQ的长为y．

(1) 求∠C的度数；

(2) 求y与x的函数关系式．

【考点】

函数解析式; 分段函数; 动点问题的函数图象;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 已知函数表达式 $\text{[math]}$ .

(1) 在下表的两个空格中分别填入适当的数；

x	5		500	5000	50000	…
$\text{[math]}$		1.2	1.02	1.002	1.0002	…

(2) 观察上表可知，当x的值越来越大时，对应的y值越来越接近于一个常数，这个常数是什么?

综合题普通

2. 动点P在□ABCD边上沿着A→B→C→D的方向匀速移动，到达点D时停止移动.已知P的速度为1个单位长度/s，其所在位置用点P表示，P到对角线BD的距离（即垂线段PQ的长）为d个单位长度，其中d与t的函数图象如图2所示.

(1) 若a＝3，求当t＝8时△BPQ的面积；

(2) 如图3，点M，N分别在函数第一和第三段图象上，线段MN平行于横轴，M、N的横坐标分别为t₁、t₂ ，设t₁、t₂时点P走过的路程分别为 $\text{[math]}$ ，若 $\text{[math]}$ ＝ 16，求t₁、t₂的值.

综合题普通

3. 如图，在Rt△ABC中，∠C=90°，AC=8，BC=6，点P在AB上，AP=2，点E、F同时从点P出发，分别沿PA、PB以每秒1个单位长度的速度向点A、B匀速运动，点E到达点A后立刻以原速度沿AB向点B运动，点F运动到点B时停止，点E也随之停止．在点E、F运动过程中，以EF为边作正方形EFGH，使它与△ABC在线段AB的同侧．设E、F运动的时间为t/秒（t＞0），正方形EFGH与△ABC重叠部分面积为S．

(1) 当时t=1时，正方形EFGH的边长是．当t=3时，正方形EFGH的边长是

(2) 当0＜t≤2时，求S与t的函数关系式；

(3) 直接答出：在整个运动过程中，当t为何值时，S最大？最大面积是多少？

综合题困难