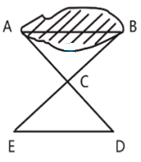
如图，为了测出池塘两端 A， B 的距离，小红在地面上选择了点 O， D， C，使，且点 A， O， C 和点 B， O， D 分别都在一条直线上. 小红认为只要量出 D， C 的距离，就能知道 A， B 的距离. 此方法的原理是全等三角形的判定定理，其依据是（）

0 返回首页

1. 如图，为了测出池塘两端 A， B 的距离，小红在地面上选择了点 O， D， C，使 $\text{[math]}$ ，且点 A， O， C 和点 B， O， D 分别都在一条直线上. 小红认为只要量出 D， C 的距离，就能知道 A， B 的距离. 此方法的原理是全等三角形的判定定理，其依据是（）

A. SSS B. SAS C. ASA D. AAS

【考点】

三角形全等的判定-SAS; 对顶角及其性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

单选题普通

基础巩固

能力提升

变式训练

拓展培优

真题演练

换一批

1. 如图，由 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，得 $\text{[math]}$ 的根据是（　　）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易

2. 如图，在△ABC和△DEF中，AB＝DE，AB $\text{[math]}$ DE，运用“SAS”判定△ABC≌△DEF，需补充的条件是（　　）

A. AC＝DF B. ∠A＝∠D C. BE＝CF D. ∠ACB＝∠DFE

单选题容易

3. 如图，已知 $\text{[math]}$ ，则 $\text{[math]}$ 的根据是（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易

1. 如图，小亮要测量水池的宽度 $\text{[math]}$ ，但没有足够长的绳子，聪明的他设计了如下方案及方案的依据．现需要回答横线上符号表示的内容：

（1）先在地上取一个可以直接到达A点和 $\text{[math]}$ 点的点 $\text{[math]}$ ；

（2）连接 $\text{[math]}$ 并延长到 $\text{[math]}$ ，使得 △

（3）连接 $\text{[math]}$ 并延长到 $\text{[math]}$ ，使得 ▽

（4）连接 ○ 并测量出它的长度，就是水池的宽度 $\text{[math]}$ ．

（5）上述方案的依据是 ◇ ．

其中错误的选项是（）

A. △代表 $\text{[math]}$ B. ▽代表 $\text{[math]}$ C. ○代表 $\text{[math]}$ D. ◇代表 $\text{[math]}$

单选题普通

2. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 上一点， $\text{[math]}$ ，已知 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题普通

3. 如图，在 $\text{[math]}$ 的正方形网格中，每个小正方形的边长都为1，则 $\text{[math]}$ 和 $\text{[math]}$ 的关系为（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题普通

1. （填空题，其中括号里填写推理依据）如图， $\text{[math]}$ ， $\text{[math]}$ 相交于点O， $\text{[math]}$ ．求证： $\text{[math]}$ ．

分析：要证 $\text{[math]}$ ，只要证 $\text{[math]}$ ______ ．

证明：

在 $\text{[math]}$ 与 $\text{[math]}$ 中，

$\text{[math]}$

∴ $\text{[math]}$ ______（_______），

∴ $\text{[math]}$ （_______）．

填空题普通

2. 如图，若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的度数为．

填空题容易

3. 如图，已知 $\text{[math]}$ ，只需补充条件，就可以根据“ $\text{[math]}$ ”判定 $\text{[math]}$

填空题容易

1. 某校项目式学习小组开展项目活动，过程如下：

项目主题：测量某水潭的宽度．

问题驱动：能利用哪些数学原理来测量水潭的宽度？

组内探究：由于水潭中间不易到达，无法直接测量，需要借助一些工具来测量，比如自制的直角三角形硬纸板，米尺，测角仪，平面镜等，甚至还可以利用无人机，确定方法后，先画出测量示意图，然后进行实地测量，并得到具体数据，从而计算水潭的宽度．

成果展示：下面是同学们进行交流展示时的两种测量方案：

方案	方案①	方案②
测量示意图
测量说明	如图①，测量员在地面上找一点 $\text{[math]}$ ，在 $\text{[math]}$ 连线的中点 $\text{[math]}$ 处做好标记，从点 $\text{[math]}$ 出发，沿着与 $\text{[math]}$ 平行的直线向前走到点 $\text{[math]}$ 处，使得点 $\text{[math]}$ 与点 $\text{[math]}$ 、 $\text{[math]}$ 在一条直线上，测出 $\text{[math]}$ 的长度	如图②，测量员在地面上找一点 $\text{[math]}$ ，沿着 $\text{[math]}$ 向前走到点 $\text{[math]}$ 处，使得 $\text{[math]}$ ，沿着 $\text{[math]}$ 向前走到点 $\text{[math]}$ 处，使得 $\text{[math]}$ ，测出 $\text{[math]}$ 、 $\text{[math]}$ 两点之间的距离
测量结果	$\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$	$\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$