1.
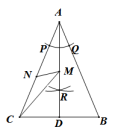
如图,在△ABC中,AB=AC.在AB、AC上分别截取AP、AQ,使AP=AQ.再分别以点P,Q为圆心,以大于 PQ的长为半径作弧,两弧在∠BAC内交于点R,作射线AR,交BC于点D.已知BC=5,AD=6.若点M、N分别是线段AD和线段AC上的动点,则CM+MN的最小值为( )
PQ的长为半径作弧,两弧在∠BAC内交于点R,作射线AR,交BC于点D.已知BC=5,AD=6.若点M、N分别是线段AD和线段AC上的动点,则CM+MN的最小值为( )
A.
4
B.
5
C.
 D.
2
D.
2
【考点】
勾股定理;
轴对称的应用-最短距离问题;
基础巩固
能力提升
变式训练
拓展培优
真题演练