1.
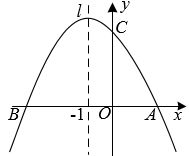
如图，二次函数
的图象与x轴交于A、B两点（点A在点B的右侧），与y轴交于点C．
(1)
求点A、B、C的坐标；
(2)
若点M在抛物线的对称轴上，且△MAC的周长最小，求点M的坐标；
(3)
若点P在x轴上，且△PBC为等腰三角形，请求出所有符合条件的点P的坐标．
【考点】
二次函数图象与坐标轴的交点问题;
等腰三角形的性质;
勾股定理;
轴对称的应用-最短距离问题;
二次函数y=ax²+bx+c的性质;
