1.
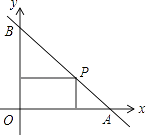
如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为10,则该直线的函数表达式是( )
A.
y=x+5
B.
y=x+10
C.
y=﹣x+5
D.
y=﹣x+10
【考点】
待定系数法求一次函数解析式;
矩形的性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练