0 返回首页
浙教版2018-2019学年重点高中自主招生数学模拟试卷（四）
共 22 题 ; 386人浏览 ; 中考阶段
2019-05-28
发布测评 / 在线自测
一、选择题 (共10题，共30分)
1. 如果一个三角形的三边长分别为1，k，3，则化简 的结果是（   ）
A. ﹣5 B. 1 C. 13 D. 19﹣4k
单选题 普通
2. 设x为正整数，若x+1是完全平方数，则它前面的一个完全平方数是（   ）
A. x B. C. D.
单选题 普通
3. (2017·达州模拟)如图，A，B，C，D是直线L上顺次四点，M，N分别是AB，CD的中点，且MN=6cm，BC=1cm，则AD的长等于（   ）

A. 10cm B. 11cm C. 12cm D. 13cm
单选题 容易
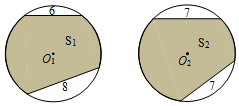
4. 如图，⊙O1与⊙O2的半径均为5，⊙O1的两条弦长分别为6和8，⊙O2的两条弦长均为7，则图中阴影部分面积的大小关系为（   ）

A. S1＞S2 B. S1＜S2 C. S1=S2 D. 无法确定
单选题 普通
5. 已知x=2是关于x的一元一次方程mx+2=0的解，则m的值为（   ）
A. ﹣1 B. 0 C. 1 D. 2
单选题 容易
6. 某单位在一快餐店订了22盒盒饭，共花费183元，盒饭共有甲、乙、丙三种，它们的单价分别为10元、8元、5元．那么可能的不同订餐方案有（　　）

A. 1个 B. 2个 C. 3个 D. 4个
单选题 普通
7. 如图，点C为线段AB上一点，且AC=2CB，以AC、CB为边在AB的同侧作等边△ADC和等边△EBC，连接DB、AE交于点F，连接FC，若FC=3，设DF=a、EF=b，则a、b满足（   ）

A. a=2b+1 B. a=2b+2 C. a=2b D. a=2b+3
单选题 普通
8. 设关于x的方程ax2+（a+2）x+9a=0，有两个不相等的实数根x1、x2 ， 且x1＜1＜x2 ， 那么实数a的取值范围是（   ）
A. B. C. D.
单选题 普通
9. (2018·沧州模拟)如图，已知在△ABC中，点D，E分别在边AB，AC上，DE∥BC，AD：BD=2：1，点F在AC上，AF：FC=1：2，联结BF，交DE于点G，那么DG：GE等于（   ）

A. 1：2 B. 1：3 C. 2：3 D. 2：5．
单选题 普通
10. 7条长度均为整数厘米的线段：a1 ， a2 ， a3 ， a4 ， a5 ， a6 ， a7 ， 满足a1＜a2＜a3＜a4＜a5＜a6＜a7 ， 且这7条线段中的任意3条都不能构成三角形．若a1=1厘米，a7=21厘米，则a6能取的值是（   ）
A. 18厘米 B. 13厘米 C. 8厘米 D. 5厘米
单选题 普通
二、填空题 (共8题，共40分)
11. (2018·黔西南模拟)若不等式组 无解，则m的取值范围是．
填空题 普通
12. 如图，在平面直角坐标系中，已知点A的坐标是（4，0），并且OA=OC=4OB，动点P在过A，B，C三点的抛物线上．过点P作PE垂直于y轴于点E，交直线AC于点D，过点D作x轴的垂线．垂足为F，连接EF，当线段EF的长度最短时，点P的坐标为．

填空题 普通
13.

如图，在菱形ABCD中，DE⊥AB ， 垂足是E ， DE=6，sinA= ，则菱形ABCD的周长是
填空题 普通
14. 已知asinθ+cosθ=1，且bsinθ﹣cosθ=1，（其中θ是锐角），则ab=．
填空题 普通
15. 设x是实数，则函数y=|x﹣1|+|x﹣2|﹣|x﹣3|的最小值是．
填空题 普通
16. 如图，在Rt△ABC中，∠BAC=90°，若AB=3cm，BC=5cm，E在AB上且AE=1cm，点P从B点出发，以1cm/s的速度沿BC→CA运动至A点停止，设运动的时间为ts，当t=，△BEP为等腰三角形．

填空题 普通
17. 方程x2﹣4x+3a2﹣2=0在区间[﹣1，1]上有实根．则实数a的取值范围是．
填空题 普通
18. 如图，在Rt△ABC中，∠C＝90°，BC＝a0 ， ∠A＝θ（其中a0 ， θ为常数），把边长依次为a1 ， a2 ， a3 ， …，a10的10个正方形依次放入Rt△ABC中，第一个正方形CM1P1N1的顶点分别放在Rt△ABC的各边上；第二个正方形M1M2P2N2的顶点分别放在Rt△AP1M1的各边上，…，其他正方形依次放入，则第10个正方形的边长a10＝．（用a0 ， θ表示）

填空题 普通
三、解答题 (共4题，共53分)
19. 设x1 ， x2是关于x的一元二次方程x2+2ax+a2+4a﹣2=0的两实根，当a为何值时，x12+x22有最小值？最小值是多少？
解答题 普通
20. 如图1，等腰直角三角形ABC的腰长是2，∠ABC=90度．以AB为直径作半圆O，M是BC上一动点（不运动至B、C两点），过点M引半圆为O的切线，切点是P，过点A作AB的垂线AN，交切线MP于点N，AC与ON、MN分别交于点E、F．

(1) 证明：△MON是直角三角形；
(2) 当BM= 时，求 的值（结果不取近似值）；
(3) 当BM= 时（图2），判断△AEO与△CMF是否相似？如果相似，请证明；如果不相似，请说明理由．
综合题 普通
21. 如图1，在平面直角坐标系xOy中，直线l： 与x轴、y轴分别交于点A和点B（0，﹣1），抛物线 经过点B，且与直线l的另一个交点为C（4，n）．

(1) 求n的值和抛物线的解析式；
(2) 点D在抛物线上，且点D的横坐标为t（0＜t＜4）．DE∥y轴交直线l于点E，点F在直线l上，且四边形DFEG为矩形（如图2）．若矩形DFEG的周长为p，求p与t的函数关系式以及p的最大值；
(3) M是平面内一点，将△AOB绕点M沿逆时针方向旋转90°后，得到△A1O1B1 ， 点A、O、B的对应点分别是点A1、O1、B1 ． 若△A1O1B1的两个顶点恰好落在抛物线上，请直接写出点A1的横坐标．
综合题 困难
22. 如图，已知二次函数y=﹣x2+bx+c（c＞0）的图象与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，且OB=OC=3，顶点为M．

(1) 求二次函数的解析式；
(2) 点P为线段BM上的一个动点，过点P作x轴的垂线PQ，垂足为Q，若OQ=m，四边形ACPQ的面积为S，求S关于m的函数解析式，并写出m的取值范围；
(3) 探索：线段BM上是否存在点N，使△NMC为等腰三角形？如果存在，求出点N的坐标；如果不存在，请说明理由．
综合题 困难