1.
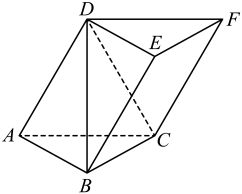
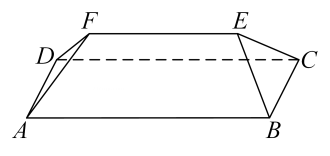
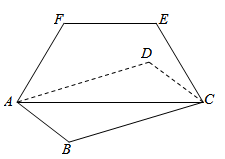
如图,在四棱锥P一ABCD中,平面PAB⊥平面ABCD, AB⊥BC, AD//BC, AD=3,PA=BC=2AB=2,
PB= .

(Ⅰ)求证:BC⊥PB;
(Ⅱ)求二面角P一CD一A的余弦值;
(Ⅲ)若点E在棱PA上,且BE//平面PCD,求线段BE的长.
【考点】
二面角及二面角的平面角;