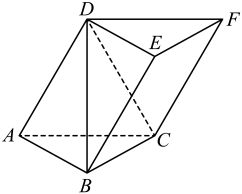
如图，在斜三棱柱中，底面ABC是边长为2的正三角形，，侧棱AD与底面ABC所成角为60°．

1. 如图，在斜三棱柱 $\text{[math]}$ 中，底面ABC是边长为2的正三角形， $\text{[math]}$ ，侧棱AD与底面ABC所成角为60°．

(1) 求证：四边形BCFE为矩形；

(2) 求平面DBC与平面BCFE夹角的余弦值．

【考点】

二面角及二面角的平面角;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. 如图，在三棱锥 $\text{[math]}$ 中， $\text{[math]}$ ．

(1) 求证： $\text{[math]}$ ；

(2) 求二面角 $\text{[math]}$ 的余弦值．

解答题普通

2. 如图，在四棱锥 $\text{[math]}$ 中，底面 $\text{[math]}$ 为菱形， $\text{[math]}$ 为 $\text{[math]}$ 上一点.

(1) 若 $\text{[math]}$ 平面 $\text{[math]}$ ，试说明点 $\text{[math]}$ 的位置并证明的结论；

(2) 若 $\text{[math]}$ 为 $\text{[math]}$ 的中点， $\text{[math]}$ 平面 $\text{[math]}$ ，且 $\text{[math]}$ ，

求二面角 $\text{[math]}$ 的余弦值.

解答题普通

3. 如图，在四棱锥P一ABCD中，平面PAB⊥平面ABCD， AB⊥BC， AD//BC， AD=3，PA=BC=2AB=2，

PB＝ $\text{[math]}$ ．

(Ⅰ)求证：BC⊥PB；

(Ⅱ)求二面角P一CD一A的余弦值；

(Ⅲ)若点E在棱PA上，且BE//平面PCD，求线段BE的长．

解答题普通