1.
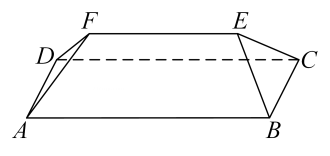
坡屋顶是我国传统建筑造型之一,蕴含着丰富的数学元素.安装灯带可以勾勒出建筑轮廓,展现造型之美.如图,某坡屋顶可视为一个五面体,其中两个面是全等的等腰梯形,两个面是全等的等腰三角形.若 , 且等腰梯形所在的平面、等腰三角形所在的平面与平面
, 且等腰梯形所在的平面、等腰三角形所在的平面与平面 的夹角的正切值均为
的夹角的正切值均为 , 则该五面体的所有棱长之和为( )
, 则该五面体的所有棱长之和为( )
A.
 B.
B.
 C.
C.
 D.
D.

【考点】
二面角及二面角的平面角;








