1.
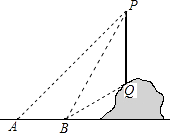
2018年4月12日,菏泽国际牡丹花会拉开帷幕,菏泽电视台用直升机航拍技术全程直播.如图,在直升机的镜头下,观测曹州牡丹园A处的俯角为30°,B处的俯角为45°,如果此时直升机镜头C处的高度CD为200米,点A、B、D在同一条直线上,则A、B两点间的距离为多少米?(结果保留根号)

【考点】
解直角三角形;
解直角三角形的实际应用﹣仰角俯角问题;