1.
如图,平面直角坐标系  中,点
中,点  的坐标为
的坐标为  ,
,  轴,垂足为
轴,垂足为  ,点
,点  从原点
从原点  出发向
出发向  轴正方向运动,同时,点
轴正方向运动,同时,点  从点
从点  出发向点
出发向点  运动,当点
运动,当点  到达点
到达点  时,点
时,点  、
、  同时停止运动,若点
同时停止运动,若点  与点
与点  的速度之比为
的速度之比为  ,则下列说法正确的是( )
,则下列说法正确的是( )
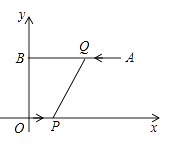
A.
线段  始终经过点
始终经过点  B.
线段
B.
线段  始终经过点
始终经过点  C.
线段
C.
线段  始终经过点
始终经过点  D.
线段
D.
线段  不可能始终经过某一定点
不可能始终经过某一定点
【考点】
两一次函数图象相交或平行问题;
一次函数中的动态几何问题;
基础巩固
能力提升
变式训练
拓展培优







