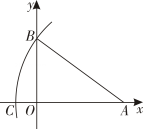
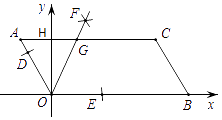
菱形OABC在平面直角坐标系中的位置如图所示.∠AOC=45°，OC= ，则点B的坐标为( )

1. 菱形OABC在平面直角坐标系中的位置如图所示.∠AOC=45°，OC= $\text{[math]}$ ，则点B的坐标为( )

A. ( $\text{[math]}$ ， 1). B. (1， $\text{[math]}$ ). C. ( $\text{[math]}$ +1，1). D. (1， $\text{[math]}$ +1).

【考点】

坐标与图形性质; 勾股定理; 平行四边形的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

单选题普通

1. 在直角三角形中，若勾为3，股为4，则弦为（）

A. 5 B. 6 C. 7 D. 8

单选题容易

2. 如图，这是一个利用平面直角坐标系画出的某学校的示意图，如果这个坐标系分别以正东、正北都向为 $\text{[math]}$ 轴、 $\text{[math]}$ 轴的正方向，并且综合楼和食堂的坐标分别是 $\text{[math]}$ 和 $\text{[math]}$ ，则教学楼的坐标是（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易

3. 在平面直角坐标系中，点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，则线段 $\text{[math]}$ 上任意一点的坐标可表示为（　　）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易