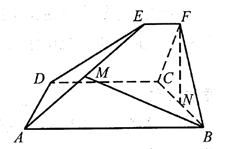
如图，已知矩形所在平面与等腰直角三角形所在平面互相垂直，，，为线段的中点．（Ⅰ）证明：；（Ⅱ）求与平面所成的角的余弦值．

1. 如图，已知矩形 $\text{[math]}$ 所在平面与等腰直角三角形 $\text{[math]}$ 所在平面互相垂直， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为线段 $\text{[math]}$ 的中点．

（Ⅰ）证明： $\text{[math]}$ ；

（Ⅱ）求 $\text{[math]}$ 与平面 $\text{[math]}$ 所成的角的余弦值．

【考点】

直线与平面垂直的判定;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. 已知三棱锥A﹣BPC中，AP⊥PC，AC⊥BC，M为AB的中点，D为PB的中点，且△PMB为正三角形．

(1) 求证：BC⊥平面APC；

(2) 若BC=3，AB=10，求三棱锥B﹣MDC的体积V_B_﹣_MDC ．

解答题普通