1.
为建设全域旅游西昌,加快旅游产业发展. 年
年 月
月 日位于西昌主城区东部的历史风貌核心区唐园正式开园,坐落于唐园内的怀远塔乃唐园至高点,为七层密檐式八角砖混结构阁楼式塔楼,建筑面积为
日位于西昌主城区东部的历史风貌核心区唐园正式开园,坐落于唐园内的怀远塔乃唐园至高点,为七层密檐式八角砖混结构阁楼式塔楼,建筑面积为 平方米,塔顶金碧辉煌,为“火珠垂莲”窣(
平方米,塔顶金碧辉煌,为“火珠垂莲”窣( )堵坡造型.某校为了让学生进一步了解怀远塔,组织九年级(
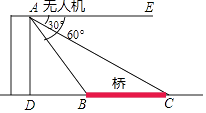
)堵坡造型.某校为了让学生进一步了解怀远塔,组织九年级( )班学生利用综合实践课测量怀远塔的高度.小江同学站在如图所示的怀远塔前的平地上
)班学生利用综合实践课测量怀远塔的高度.小江同学站在如图所示的怀远塔前的平地上 点处,测得塔顶
点处,测得塔顶 的仰角为
的仰角为 , 眼睛
, 眼睛 距离地面
距离地面 , 向塔前行
, 向塔前行 , 到达点
, 到达点 处,测得塔顶
处,测得塔顶 的仰角为
的仰角为 , 求塔高
, 求塔高 . (参考数据:
. (参考数据: , 结果精确到
, 结果精确到 )
)

【考点】
解直角三角形的实际应用﹣仰角俯角问题;
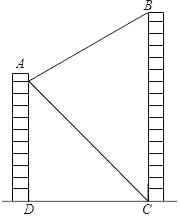
 , 在与山脚C距离200米的D处,测得山顶A的仰角为26.6°,求小山岗的高AB(结果取整数:参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50).
, 在与山脚C距离200米的D处,测得山顶A的仰角为26.6°,求小山岗的高AB(结果取整数:参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50).