1.
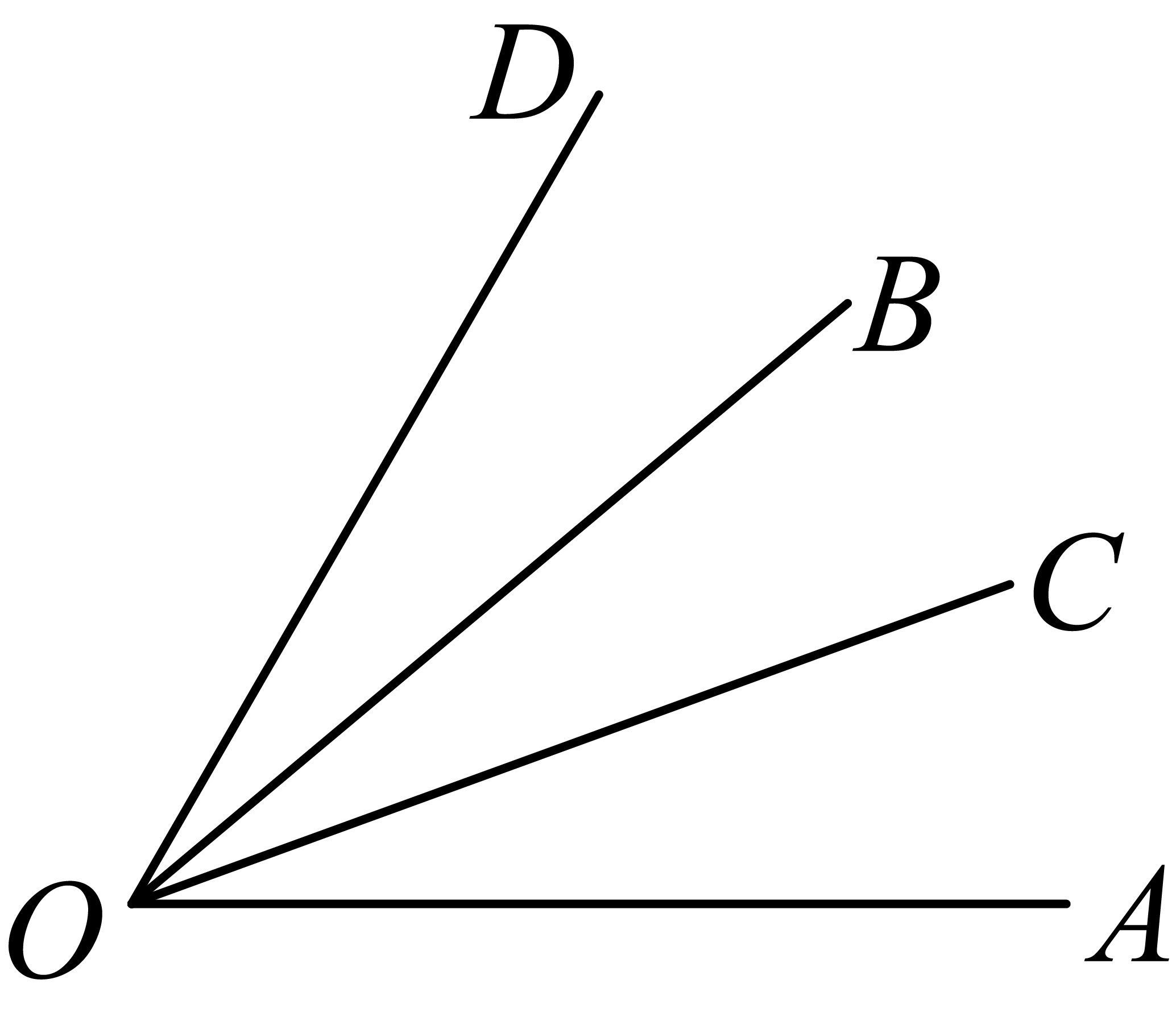
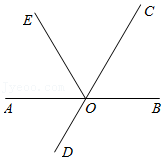
如图,已知∠AOB=90°,OC 是∠AOB 内任意一条射线,OB,OD 分别平分∠COD,∠BOE,有下列结论:①∠COD=∠BOE;②∠COE =3∠BOD;③∠BOE=∠AOC;④∠AOC+∠BOD=90°。其中正确的是 ( )

A.
①②④
B.
①③④
C.
①②③
D.
②③④
【考点】
角的运算;
角平分线的概念;
基础巩固
能力提升
变式训练
拓展培优
真题演练