1.
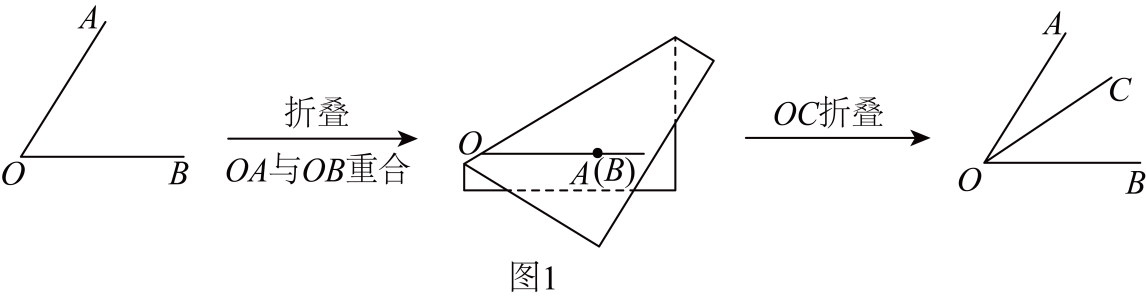
已知长方形纸片ABCD,点E在边AB 上,点F,G在边CD上,连结EF,EG.将  对折,点B 落在直线EG 上的点,
对折,点B 落在直线EG 上的点,  处,得折痕 EM;将
处,得折痕 EM;将  对折,点A 落在直线EF 上的点.
对折,点A 落在直线EF 上的点.  处,得折痕 EN.
处,得折痕 EN.

(1)
如图1,若点 F 与点G 重合,求  的度数.
(2)
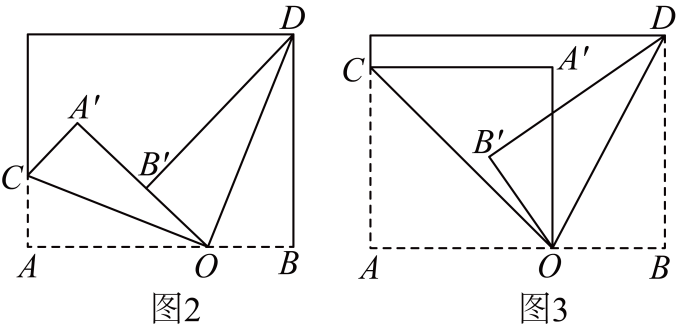
如图2,若点 G 在点 F 的右侧,且.
的度数.
(2)
如图2,若点 G 在点 F 的右侧,且.  求
求  的度数.
(3)
若
的度数.
(3)
若  , 请直接用含α的式子表示
, 请直接用含α的式子表示  的大小.
的大小.
【考点】
角的运算;
翻折变换(折叠问题);
角平分线的概念;