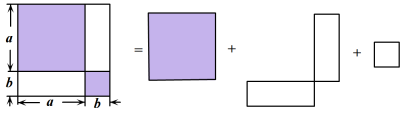
某中学开展以“杭州亚运会”为主题的学科活动，要求设计几何图形作品来表达对亚运会的祝福．小冬以长方形的四条为边分别向外作四个正方形，设计出“中”字图案，如图所示．若长方形的相邻两边之差为6，且四个正方形的面积和为100，则长方形的面积是（）

0 返回首页

1. 某中学开展以“杭州亚运会”为主题的学科活动，要求设计几何图形作品来表达对亚运会的祝福．小冬以长方形 $\text{[math]}$ 的四条为边分别向外作四个正方形，设计出“中”字图案，如图所示．若长方形 $\text{[math]}$ 的相邻两边之差为6，且四个正方形的面积和为100，则长方形 $\text{[math]}$ 的面积是（）

A. 7 B. 8 C. 9 D. 10

【考点】

完全平方公式的几何背景;

【答案】

您现在未登录，无法查看试题答案与解析。登录

单选题容易

基础巩固

能力提升

变式训练

拓展培优

真题演练

换一批

1. 如图，可验证的乘法公式是（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易

2. 你能根据下图中图形的面积关系得到的数学公式是（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易

3. 如图，线段 $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 中点，点 $\text{[math]}$ 在线段 $\text{[math]}$ 上， $\text{[math]}$ ，如图所示构造三个正方形．若阴影部分的面积为8，且 $\text{[math]}$ ，则小正方形的边长为（）．

A. 3 B. $\text{[math]}$ C. 7 D. $\text{[math]}$

单选题容易

1. 小冬以长方形 $\text{[math]}$ 的四条边为边向外作四个正方形，设计出“中”字图案，如图所示．若四个正方形的周长之和为40，面积之和为26，则长方形 $\text{[math]}$ 的面积为（）

A. 6 B. 8 C. 10 D. 12

单选题普通

2. 已知长方形 $\text{[math]}$ 可以按图示方式分成九部分，在 $\text{[math]}$ ， $\text{[math]}$ 变化的过程中，下面说法正确的有（）

①长方形 $\text{[math]}$ 的长宽之比可能为2

②图中存在三部分的周长之和恰好等于长方形 $\text{[math]}$ 的周长

③当长方形 $\text{[math]}$ 为正方形时，九部分都为正方形

④当长方形 $\text{[math]}$ 的周长为60时，它的面积可能为100

A. ②③ B. ①③ C. ②③④ D. ①③④

单选题普通

3. 如图，在一块边长为a的正方形花圃中，两纵两横的4条宽度为b的人行道把花圃分成9块，下面是四种计算种花部分土地总面积的代数式：①（a﹣2b）²；②a²﹣4ab；③a²﹣4ab+b²；④a²﹣4ab+4b² ．其中正确的有（　　）

A. ② B. ①③ C. ①④ D. ④

单选题普通

1. 小聪在学习完乘法公式后，发现完全平方公式经过适当的变形或数形结合，可以解决很多数学问题．如图摆放两个正方形卡片， $\text{[math]}$ 在同一直线上．若 $\text{[math]}$ ，且两个正方形面积之和为13，则阴影部分的面积为．

填空题容易

2. 如图，边长为 $\text{[math]}$ 的正方形纸片剪出一个边长为 $\text{[math]}$ 的正方形之后，剩余部分可剪拼成一个长方形，若拼成的长方形一边长为4，则另一边长为16，求 $\text{[math]}$ 的值．

填空题普通

3. 【知识回顾】数形结合是数学学习的一种重要的思想方法，借助图的直观性，可以帮助理解数学问题．图①中阴影部分的面积能解释的乘法公式为__________；图②中阴影部分的面积能解释的乘法公式为__________．

【拓展探究】用4个全等的长和宽分别为a、b的长方形拼摆成一个如图③的正方形．

（1）通过计算阴影部分的面积，直接写出这三个代数式 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的等量关系．

（2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的值．

【解决问题】如图④，C是线段 $\text{[math]}$ 上的一点，分别以 $\text{[math]}$ 为边向两边作正方形 $\text{[math]}$ 和 $\text{[math]}$ ，设 $\text{[math]}$ ，两正方形的面积和为20，求 $\text{[math]}$ 的面积．

解答题普通

1. 四边形 $\text{[math]}$ 和四边形 $\text{[math]}$ 都是正方形、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 三点在同一直线上．

(1) 如图1，点 $\text{[math]}$ 在线段 $\text{[math]}$ 上，点 $\text{[math]}$ 在线段 $\text{[math]}$ 上，延长 $\text{[math]}$ ， $\text{[math]}$ 分别交 $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．

①若 $\text{[math]}$ ，求三角形 $\text{[math]}$ 的面积；

②若正方形 $\text{[math]}$ 和正方形 $\text{[math]}$ 的边长分别为 $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ ，记三角形 $\text{[math]}$ 的面积为 $\text{[math]}$ ，四边形 $\text{[math]}$ 的面积为 $\text{[math]}$ ，用含有 $\text{[math]}$ ， $\text{[math]}$ 的代数式表示 $\text{[math]}$ ，并求出 $\text{[math]}$ 的值；