1.
一个容积为 的瓶子未开封时相关数据如图
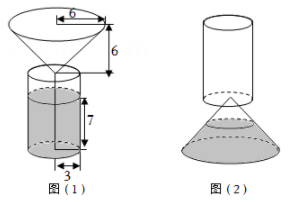
的瓶子未开封时相关数据如图 所示.将溶液倒出部分后,液面恰好在瓶身与瓶颈的交接处,此时溶液高度为
所示.将溶液倒出部分后,液面恰好在瓶身与瓶颈的交接处,此时溶液高度为 (如图2).将图2中的瓶子倒放时,溶液高度为
(如图2).将图2中的瓶子倒放时,溶液高度为 (如图3).则图2中溶液的体积为
(如图3).则图2中溶液的体积为  , 图
, 图 中溶液的体积为
中溶液的体积为 .
.

【考点】
圆柱的体积;
基础巩固
能力提升
变式训练
拓展培优
真题演练