1.
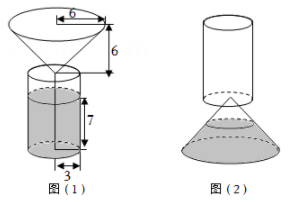
当水面距离容器口 时,乌鸦就能喝到水了.它至少要衔多少立方厘米的小石头放进瓶里才能喝到水呢?(
时,乌鸦就能喝到水了.它至少要衔多少立方厘米的小石头放进瓶里才能喝到水呢?( 取3.14)
取3.14)

【考点】
圆柱的体积;
基础巩固
能力提升
变式训练
拓展培优
真题演练