0 返回首页
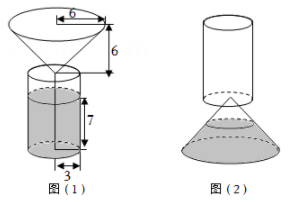
1.  一个盛有水的圆柱形容器，底面半径为10厘米，高30厘米，水深12厘米．今将一个底面直径2厘米，高为6厘米的圆锥形铁块放入这个圆柱形容器中，这时圆柱形容器的水深是多少厘米？
【考点】
圆柱的体积;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
解答题 普通
基础巩固
能力提升
变式训练
拓展培优
真题演练
换一批
1. 有一个圆锥形的小麦堆，底面周长是18.84米，高1.5米，把这些小麦全部装入一个底面直径是3米的圆柱粮囤，结果最上面的小麦离囤口还有0.3米．求这个粮囤的高．
综合题 容易
2. 如图是一个底面半径为3厘米的圆柱木块被削去一半后的形状，请你计算出它的体积．（圆周率取3.14）


       
解答题 容易
3. 下面是一个圆柱表面展开图，求这个圆柱的体积．

   
解答题 容易