1.
如图,在矩形 中,点
中,点 在
在 边上,把
边上,把 沿直线
沿直线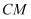 折叠,使点
折叠,使点 落在
落在 边上的点
边上的点 处,连接
处,连接 , 过点
, 过点 作
作 , 垂足为
, 垂足为 , 若
, 若 ,
,  , 则线段
, 则线段 的长是.
的长是.

【考点】
三角形全等及其性质;
勾股定理;











