1.
数学教育家波利亚曾说:“对一个数学问题,改变它的形式,变换它的结构,直到发现有价值的东西,这是数学解题的一个重要原则”.在复习二次根式时,老师提出了一个求代数式最小值的问题,如: “当 时,求代数式
时,求代数式  的最小值”,其中
的最小值”,其中  可看作两直角边分别为x和2的
可看作两直角边分别为x和2的 的斜边长,
的斜边长,  可看作两直角边分别是
可看作两直角边分别是 和3的
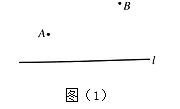
和3的 的斜边长.于是构造出如图,将问题转化为求
的斜边长.于是构造出如图,将问题转化为求 的最小值,运用此方法,请你解决问题:已知x,y均为正数,且
的最小值,运用此方法,请你解决问题:已知x,y均为正数,且 . 则
. 则  的最小值是( )
的最小值是( )

A.
 B.
B.
 C.
C.
 D.
6
D.
6
【考点】
两点之间线段最短;
勾股定理的实际应用-最短路径问题;
基础巩固
能力提升
变式训练
拓展培优