1.
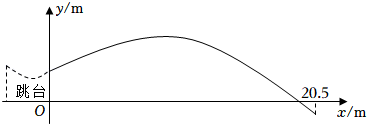
如图,水平地面点 处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为
处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为 , 小武在直线
, 小武在直线 上点
上点 (靠点
(靠点 一侧)竖直向上摆放若干个无盖的圆柱形桶,已知
一侧)竖直向上摆放若干个无盖的圆柱形桶,已知 米,
米, 米,网球飞行最大高度
米,网球飞行最大高度 米,圆柱形桶的直径为
米,圆柱形桶的直径为 米,高为
米,高为 米(网球的体积和圆柱形桶的厚度忽略不计).
米(网球的体积和圆柱形桶的厚度忽略不计).

(1)当竖直摆放8个圆柱形桶时,网球(填“能”或“不能”)落入桶内.
(2)当竖直摆放圆柱形桶至少个时,网球能落入桶内.
【考点】
二次函数的实际应用-抛球问题;