1.
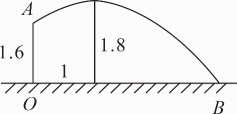
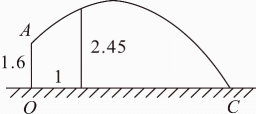
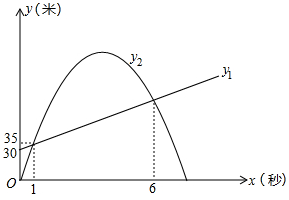
问题:如何设计击球路线?情境:某校羽毛球社团的同学们经常运用数学知识对羽毛球技术进行分析,下面是他们对击球线路的分析.如图,在平面直角坐标系中,点A在x轴上,球网AB与y轴的水平距离OA=3m,击球点P在y轴上.
击球方案:
扣球 | 羽毛球的飞行高度y(m)与水平距离x(m)近似满足一次函数关系C1:y=﹣0.4x+b,当羽毛球的水平距离为1m时,飞行高度为2.4m. |
吊球 | 羽毛球的飞行高度y(m)与水平距离x(m)近似满足二次函数关系C2 , 此时当羽毛球飞行的水平距离是1米时,达到最大高度3.2米. |
高远球 | 羽毛球的飞行高度y(m)与水平距离x(m)近似满足二次函数关系C3:y=a(x﹣n)2+h,且飞行的最大高度在4.8m和5.8m之间. |

探究:
(1)
求扣球和吊球时,求羽毛球飞行满足的函数表达式;
(2)
①若选择扣球的方式,刚好能使球过网,求球网AB的高度为多少;
(3)
通过对本次训练进行分析,若高远球的击球位置P保持不变,接球人站在离球网4m处,他可前后移动各1m,接球的高度为2.8m,要使得这类高远球刚好让接球人接到,请求出此类高远球抛物线解析式a的取值范围.
②若选择吊球的方式,求羽毛球落地点到球网的距离;
【考点】
二次函数的实际应用-抛球问题;