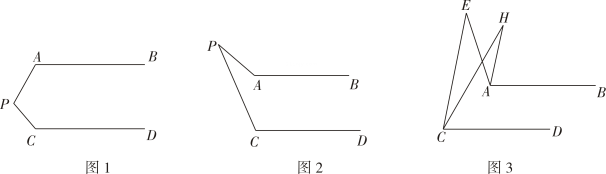
【感知】如图①，，，，的度数为______．【探究】如图②，，点P在射线上运动，，，（1）当点P在线段上运动时，试探究，，之间的数量关系．（2）当点P在线段C，D两点外侧运动时（点P与点C，D，O三点不重合），直接写出，，之间的数量关系为_____

1. 如图直线 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的度数．

解答题容易

2. 完成证明并写出推理根据：如图，直线 $\text{[math]}$ 分别与直线 $\text{[math]}$ 、 $\text{[math]}$ 交于点 $\text{[math]}$ 和点 $\text{[math]}$ ． $\text{[math]}$ ，射线 $\text{[math]}$ 、 $\text{[math]}$ 分别与直线 $\text{[math]}$ 交于点 $\text{[math]}$ 、 $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$ 与 $\text{[math]}$ 有何数量关系？并说明理由．

解： $\text{[math]}$ 与 $\text{[math]}$ 的数量关系为　　，理由如下：

$\text{[math]}$ （已知）．

∴ $\text{[math]}$ ∥　　(　　)．

$\text{[math]}$ 　　(　　)．

$\text{[math]}$ （已知），

$\text{[math]}$ 　　 $\text{[math]}$ （垂直的定义）．

$\text{[math]}$ 　　．

证明题容易

3. 如图，AB∥CD∥PN，∠ABC=50°，∠CPN=150°．求∠BCP的度数．

解答题容易

1. （ $\text{[math]}$ ）问题情境：图 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的度数.小明的思路是：过 $\text{[math]}$ 作 $\text{[math]}$ ，通过平行线性质来求 $\text{[math]}$ .按小明的思路，易求得 $\text{[math]}$ 的度数为_________；（直接写出答案）

（ $\text{[math]}$ ）问题探究：图 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 之间一点，连接 $\text{[math]}$ ，试探究 $\text{[math]}$ 与 $\text{[math]}$ ， $\text{[math]}$ 之间的数量关系；

（ $\text{[math]}$ ）图 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的度数.

实践探究题困难

2. 如图1， $\text{[math]}$ 是直线 $\text{[math]}$ 、 $\text{[math]}$ 内部一点， $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ．

(1) 探究猜想：

①若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ▲ 度；

②若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ▲ 度；

③猜想图1中 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 的数量关系并证明你的结论．

(2) 拓展应用：

如图2，射线 $\text{[math]}$ 与长方形 $\text{[math]}$ 的边 $\text{[math]}$ 交于点 $\text{[math]}$ ，与边 $\text{[math]}$ 交于点 $\text{[math]}$ ， ①②③④分别是被射线 $\text{[math]}$ 隔开的4个区域（不含边界，其中区域③、④位于直线 $\text{[math]}$ 上方）， $\text{[math]}$ 是位于以上四个区域上的点，猜想： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的关系．（直接写出结论，不要求证明）

实践探究题困难

3. 已知直线 $\text{[math]}$ ，点 $\text{[math]}$ 为直线 $\text{[math]}$ ， $\text{[math]}$ 所确定的平面内的一点，

(1) 问题提出：如图 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 求 $\text{[math]}$ 的度数；

(2) 问题迁移：如图 $\text{[math]}$ ，写出 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的数量关系，并说明理由；

(3) 问题应用：如图 $\text{[math]}$ ， $\text{[math]}$ ： $\text{[math]}$ ： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的值．

实践探究题困难

1. 如图摆放的一副学生用直角三角板， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 相交于点G，当 $\text{[math]}$ 时， $\text{[math]}$ 的度数是（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题普通

2. 某小区车库门口的曲臂道闸升降杜如图所示， $\text{[math]}$ 垂直地面 $\text{[math]}$ 于 A 点， $\text{[math]}$ 平行于地面 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的大小是（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题普通

3. 如图，已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题普通

1. 如图，已知 $\text{[math]}$ ，请回答下列问题：

(1) 直接写出图形 $\text{[math]}$ 中 $\text{[math]}$ 之间的关系是________；

(2) 直接写出图形 $\text{[math]}$ 中 $\text{[math]}$ 之间的关系是________；

(3) 探究出图形 $\text{[math]}$ 中， $\text{[math]}$ 之间的关系，并写出证明过程．

解答题普通

2. 综合与实践

台灯作为一种照明工具，适合于书桌、床头等需要局部照明的地方，它能够集中光线，使得周围环境适合于阅读、学习或工作，对于保护眼睛健康也具有重要意义．如图1是一盖可折叠台灯．图2、图3是其平面示意图，底座MN位于水平位置，支架 $\text{[math]}$ 、 $\text{[math]}$ 为固定支撑杆，支架 $\text{[math]}$ 可绕点 $\text{[math]}$ 旋转，从而调节灯光照射方向．已知灯体顶角 $\text{[math]}$ ， $\text{[math]}$ 的平分线 $\text{[math]}$ 始终与 $\text{[math]}$ 垂直．