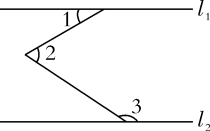
1.
补全下列推理过程:
如图,已知 ,
, 试说明:
.

解:因为(__________)
所以__________(__________)
因为(已知),
所以__________
__________(__________)
所以____________________(__________)
所以__________(__________).
因为(__________),
所以(__________).
【考点】
平行线的判定与性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练