1.
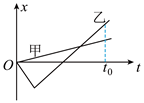
甲、乙两车在同一水平路面上做直线运动,某时刻乙车在前、甲车在后,相距s=6m,从此刻开始计时,乙车做初速度大小为12m/s加速度大小为1m/s2的匀减速直线运动,甲车运动的s-t图象如图所示(0-6s是开口向下的抛物线一部分,6-12s是直线,两部分平滑相连),求:

(1)甲车在开始计时时刻的速度v0和加速度a
(2)以后的运动过程中,两车何时相遇?
【考点】
运动学 S-t 图象;
追及相遇问题;