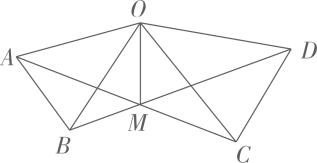
1.
如图,在 中,
中, , E是
, E是 上一点,且
上一点,且 ,
,  于E,若
于E,若 , 则
, 则 等于( )
等于( )

A.
7
B.
8
C.
9
D.
10
【考点】
角平分线的性质;
角平分线的判定;