1.
阅读下列材料,完成相应任务.
数学活动课上,老师提出了如下问题:
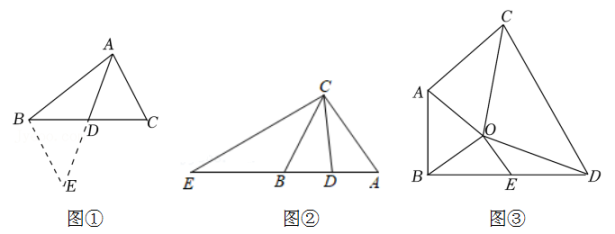
如图1,已知中,
是
边上的中线.求证:
.

智慧小组的证法如下:
证明:如图2,延长至
, 使
,
∵是
边上的中线∴
在和
中
∴ ∴
在中,
(依据一)
∴ .

任务一:上述证明过程中的“依据一”是指:____________________;
归纳总结:上述方法是通过延长中线 , 使
, 构造了一对全等三角形,将
,
,
转化到一个三角形中,进而解决问题,这种方法叫做“倍长中线法”.“倍长中线法”多用于构造全等三角形和证明边之间的关系.
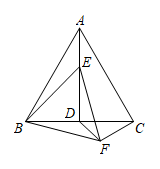
任务二:如图3, ,
, 则
的取值范围是_____________;

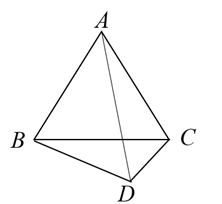
任务三:如图4,在图3的基础上,分别以和
为边作等腰直角三角形,即在
中,
,
;
中,
,
. 连接
. 试探究
与
的数量关系,并说明理由.

【考点】
三角形三边关系;
三角形全等的判定-SAS;
基础巩固
能力提升
变式训练
拓展培优
真题演练