1.
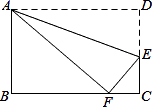
如图,一次函数y= x+b的图象与y轴交于点B(0,2),与反比例函数y=
x+b的图象与y轴交于点B(0,2),与反比例函数y= (x<0)的图象交于点D(m,n).以BD为对角线作矩形ABCD,使顶点A,C落在x轴上(点A在点C的右边),BD与AC交于点E.
(x<0)的图象交于点D(m,n).以BD为对角线作矩形ABCD,使顶点A,C落在x轴上(点A在点C的右边),BD与AC交于点E.
(1)求一次函数和反比例函数的解析式;
(2)求点A的坐标.

【考点】
勾股定理;
矩形的性质;