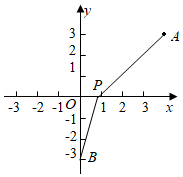若一条直线经过点(－1，1)和点(1，5)，则这条直线与x轴的交点坐标为

1. 若一条直线经过点(－1，1)和点(1，5)，则这条直线与x轴的交点坐标为

【考点】

待定系数法求一次函数解析式; 一次函数图象与坐标轴交点问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

填空题普通

1. 一次函数 $\text{[math]}$ 的图象经过点 $\text{[math]}$ ，则它与 $\text{[math]}$ 轴的交点坐标为．

填空题容易

2. 函数 $\text{[math]}$ 的图象平行于直线 $\text{[math]}$ ，且交y轴于点 $\text{[math]}$ ，则其函数表达式是．

填空题容易

3. 已知一次函数 $\text{[math]}$ 的图象经过点 $\text{[math]}$ 与 $\text{[math]}$ ，与x轴、y轴分别交于点A、点B．若坐标原点为O，则 $\text{[math]}$ 的面积为．

填空题容易