1.
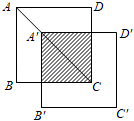
有一边长为2的正方形纸片 , 将纸片沿对角线BD剪开,再将△ABD沿射线BD的方向平移得到
, 将纸片沿对角线BD剪开,再将△ABD沿射线BD的方向平移得到 ,当△
,当△ 是等腰三角形时,△ABD平移的距离为
是等腰三角形时,△ABD平移的距离为

【考点】
正方形的性质;
平移的性质;