1.
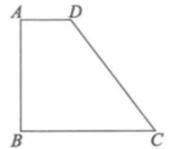
如图,某自动感应门的正上方 处装着一个感应器,该感应器的有效感应范围不超过
处装着一个感应器,该感应器的有效感应范围不超过 , 当人体进入感应器的感应范围时,感应门就会自动打开.现已知感应器离地面的高度
, 当人体进入感应器的感应范围时,感应门就会自动打开.现已知感应器离地面的高度 , 一个身高
, 一个身高 的学生
的学生 缓慢走到离门
缓慢走到离门 的地方时(
的地方时( , 假设此时人体与地面垂直),该学生头顶距离感应器多少米?感应门会自动打开吗?
, 假设此时人体与地面垂直),该学生头顶距离感应器多少米?感应门会自动打开吗?

【考点】
勾股定理;
矩形的判定与性质;