1.
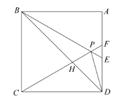
如图,矩形纸片ABCD,AD=4,AB=3,如果点E在边BC上,将纸片沿AE折叠,使点B落在点F处,连接FC,当△EFC是直角三角形时,那么BE的长为( )

A.
1.5
B.
3
C.
1.5或3
D.
有两种情况以上
【考点】
正方形的判定与性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练