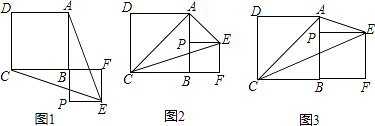
已知正方形ABCD，P为射线AB上的一点，以BP为边作正方形BPEF，使点F在线段CB的延长线上，连接EA，EC．（Ⅰ）如图1，若点P在线段AB的延长线上，求证：EA=EC；（Ⅱ）如图2，若点P在线段AB的中点，连接AC，判断△ACE的形状，并说明理由；（Ⅲ）如图3，若点P在线段AB上，连接AC，当EP平分∠AEC时，设AB=a，BP=b，求a：b及∠AEC的度数．

正方形的定义	有一组邻边相等，并且有一个角是的平行四边形叫做正方形.
正方形的性质	1.正方形的四条边，四个角都是，对角线互相垂直平分且相等，并且每一条对角线平分一组对角，它具有矩形和菱形的所有性质.
正方形的性质	2.正方形既是轴对称图形也是中心对称图形，对称轴有条，对称中心是对角线的交点.
正方形的判定	1.有一组邻边相等的矩形是正方形.
	2.有一个角是直角的是正方形.
	3.对角线互相垂直平分且相等的四边形是正方形.