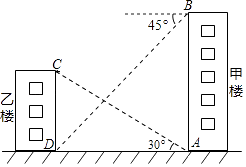
如图，用热气球的探测器测一校楼的高度，从热气球上的点测得该楼顶部点的仰角为，测得底部点的俯角为，点与楼的水平距离，则这栋楼约富度为 (结果保留根号).

0 返回首页

1. 如图，用热气球的探测器测一校楼的高度，从热气球上的点 $\text{[math]}$ 测得该楼顶部点 $\text{[math]}$ 的仰角为 $\text{[math]}$ ，测得底部点 $\text{[math]}$ 的俯角为 $\text{[math]}$ ，点 $\text{[math]}$ 与楼 $\text{[math]}$ 的水平距离 $\text{[math]}$ ，则这栋楼约富度为 $\text{[math]}$ (结果保留根号).

【考点】

解直角三角形的实际应用﹣仰角俯角问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

填空题普通

基础巩固

能力提升

变式训练

拓展培优

真题演练

换一批

1. 如图，武汉起义门城楼BC上有一旗杆AB，从与BC相距20m的D处观测旗杆顶部A的仰角为 $\text{[math]}$ ，观测旗杆底部B的仰角为 $\text{[math]}$ ，则旗杆AB的高度约为m．（结果保留小数点后一位，参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ≈1.41）．

填空题容易

2. 如图，从甲楼底部A处测得乙楼顶部C处的仰角是30°，从甲楼顶部B处测得乙楼底部D处的俯角是45°，已知甲楼的高AB是120m，则乙楼的高CD是m（结果保留根号）

填空题容易

3. 如图，一架无人机在空中A处观测到山顶B的仰角为 $\text{[math]}$ ，山顶B在水中的倒影C的俯角为 $\text{[math]}$ ，此时无人机距水面的距离 $\text{[math]}$ 米，则点B到水面距离 $\text{[math]}$ 的高度为．（参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

填空题容易

1. 在综合实践课上，数学兴趣小组用所学数学知识测量大汶河某河段的宽度.他们在河岸一侧的瞭望台上放飞一只无人机.如图，无人机在河上方距水面高60米的点 $\text{[math]}$ 处测得瞭望台正对岸 $\text{[math]}$ 处的俯角为 $\text{[math]}$ ，测得瞭望台顶端 $\text{[math]}$ 处的俯角为 $\text{[math]}$ ，已知瞭望台 $\text{[math]}$ 高12米(图中点A，B，C，P在同一平面内).那么大汶河此河段的宽AB为米.(参考数据： $\text{[math]}$ )

填空题普通

2. 综合实践课上，航模小组用无人机测量古树 $\text{[math]}$ 的高度.如图，点C处与古树底部A处在同一水平面上，且 $\text{[math]}$ 米，无人机从C处竖直上升到达D处，测得古树顶部B的俯角为 $\text{[math]}$ ，古树底部A的俯角为 $\text{[math]}$ ，则古树AB的高度约为米（结果精确到0.1米；参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）.

填空题普通

3. 如图，点 $\text{[math]}$ 位于点 $\text{[math]}$ 的北偏东 $\text{[math]}$ 相距 $\text{[math]}$ 处，点 $\text{[math]}$ 在点 $\text{[math]}$ 的正北方向，且在点 $\text{[math]}$ 的东北方向，则点 $\text{[math]}$ 到点 $\text{[math]}$ 的距离为 $\text{[math]}$ ．

填空题普通

1. 双塔是古黄河宿迁景观带的标志性建筑之一，由九层的九龙塔和七层的七风塔构成．某校数学实践小组开展测量七凤塔高度的实践活动，该小组制定了测量方案，在实地测量后撰写活动报告，报告部分内容如表：

测量七凤塔高度
测量工具	测角仪、皮尺等	活动形式	以小组为单位
测量示意图		测量步骤及结果
		如图，步骤如下： ①在C处使用测角仪测得塔的顶部点B的仰角∠BDG=37°； ②沿着CA方向走到E处，用皮尺测得CE＝24米； ③在E处使用测角仪测得塔的顶部点B的仰角∠BFG＝45°.
……