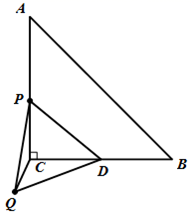
如图，某亭子的入口可以抽象成一个等边，立柱的端点D在上，且立柱与地面垂直（即，垂足为点E），则的值为（）

1. 如图，某亭子的入口可以抽象成一个等边 $\text{[math]}$ ，立柱 $\text{[math]}$ 的端点D在 $\text{[math]}$ 上，且立柱 $\text{[math]}$ 与地面垂直（即 $\text{[math]}$ ，垂足为点E），则 $\text{[math]}$ 的值为（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. 2

【考点】

等边三角形的性质; 含30°角的直角三角形;

【答案】

您现在未登录，无法查看试题答案与解析。登录

单选题容易

1. 如图，等边 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 在边 $\text{[math]}$ 上， $\text{[math]}$ ， $\text{[math]}$ ，垂足分别为 $\text{[math]}$ 、 $\text{[math]}$ ，设 $\text{[math]}$ ，若用含 $\text{[math]}$ 的式子表示 $\text{[math]}$ 的长，正确的是（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易

2. 如图，这是由6个等边三角形和1个直角三角形拼成的六边形 $\text{[math]}$ ，若中间最小的等边三角形的边长为1，则 $\text{[math]}$ 的长是（）

A. 4 B. 5 C. 6 D. 7

单选题容易

3. 如图所示，△ABC是边长为20的等边三角形，点D是BC边上任意一点，DE⊥AB于点E，DF⊥AC于点F，则BE+CF＝（　　）

A. 5 B. 10 C. 15 D. 20

单选题容易