1.
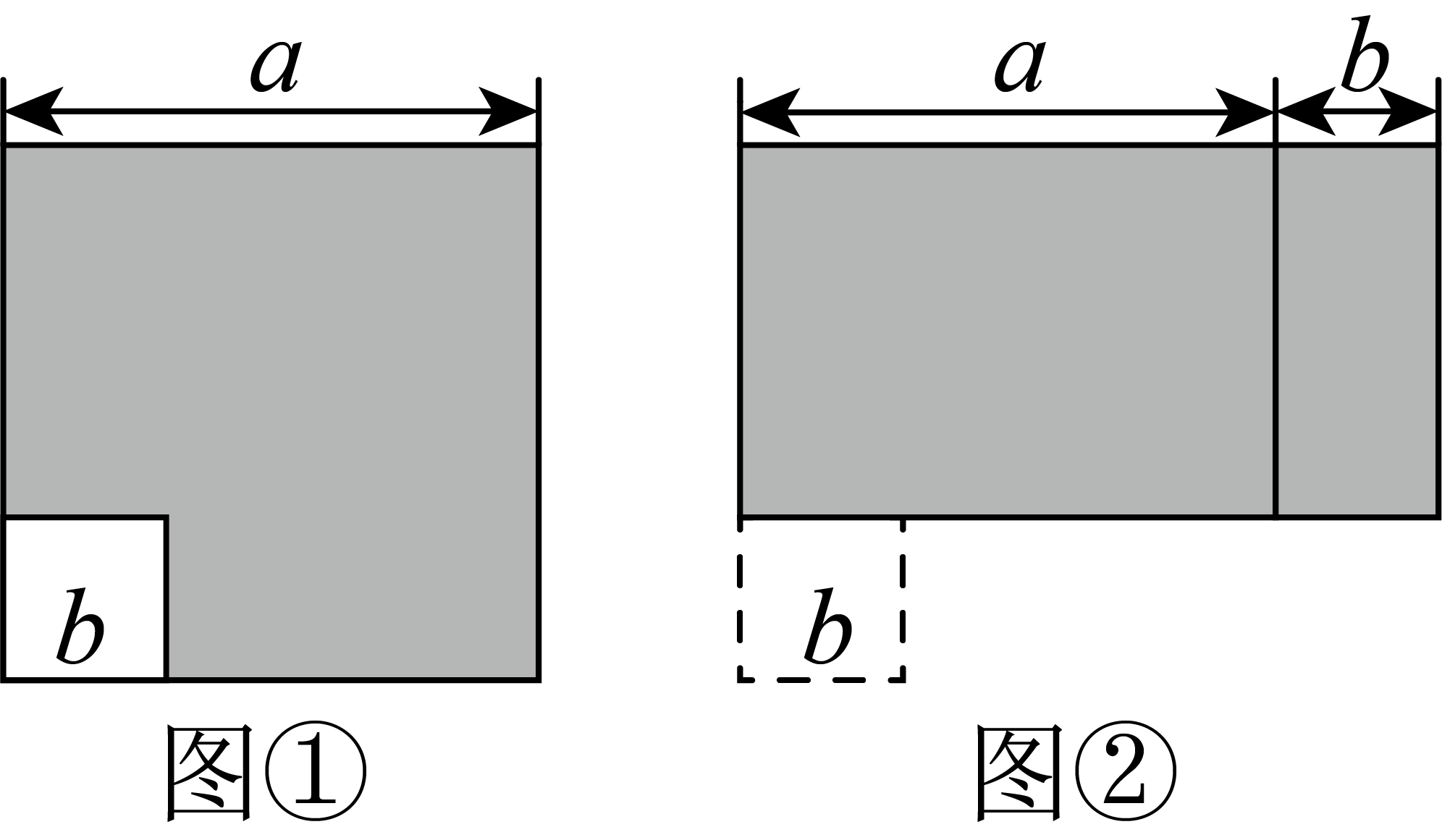
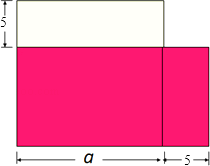
一块边长为 的正方形草坪,经过重新规划,东西方向需要加长
的正方形草坪,经过重新规划,东西方向需要加长 , 南北方向需要缩短
, 南北方向需要缩短 . 规划后的草坪面积是多少?
. 规划后的草坪面积是多少?
【考点】
平方差公式的几何背景;
基础巩固
能力提升
变式训练
拓展培优
真题演练