1.
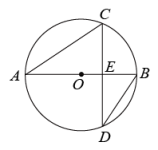
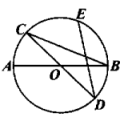
如图,AB是⊙O的弦,半径OD⊥AB,垂足为C,点E在⊙O上,连接OA、DE、BE.

(1)若∠DEB=30°,求∠AOD的度数;
(2)若CD=2,弦AB=8,求⊙O的半径长.
【考点】
垂径定理;
圆周角定理;
基础巩固
能力提升
变式训练
拓展培优
真题演练