1.
如图,⊙O是△ABC的外接圆,AB是直径,D是AC中点,直线OD与⊙O相交于E,F两点,P是⊙O外一点,P在直线OD上,连接PA,PC,AF,且满足∠PCA=∠ABC.
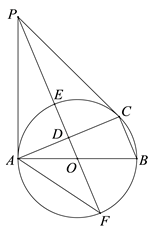
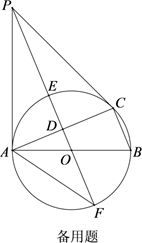
(1)
求证:PA是⊙O的切线;
(2)
证明:  ;
(3)
若BC=8,tan∠AFP=
;
(3)
若BC=8,tan∠AFP=  ,求DE的长.
,求DE的长.
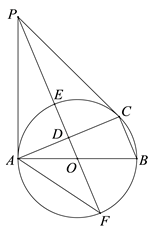
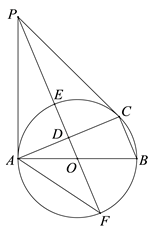
【考点】
勾股定理;
垂径定理;
圆周角定理;
切线的判定;
相似三角形的判定与性质;


