1.
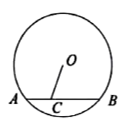
赵州桥始建于隋朝,由匠师李春设计建造,屹立千年而不倒,是我国著名的历史文物.如图为某圆弧型石拱桥的侧面图,桥的跨径 , 拱高
, 拱高 , 则拱桥的半径为m.
, 则拱桥的半径为m.

【考点】
垂径定理的实际应用;