1.
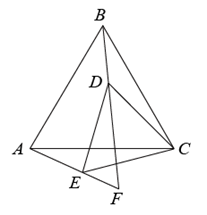
骑自行车是一种能有效改善心肺功能的耐力性有氧运动,深受大众喜爱,如图是某一自行车的平面结构示意图,已知图中的圆 (前轮),圆
(前轮),圆 (后轮)的半径均为
(后轮)的半径均为 ,
,  ,
,  ,
,  均是边长为
均是边长为 的等边三角形.设点
的等边三角形.设点 为后轮上的一点,则在骑该自行车的过程中,记
为后轮上的一点,则在骑该自行车的过程中,记 的最大值为
的最大值为 , 最小值为
, 最小值为 , 则
, 则 的值为( )
的值为( )

A.
 B.
B.
 C.
C.
 D.
D.

【考点】
等边三角形的性质;
点与圆的位置关系;
基础巩固
能力提升
变式训练
拓展培优
真题演练